Mathematical models can project how infectious diseases such as COVID-19 will likely progress in the immediate future. The
Kermack-McKendrick theory, which was developed in the 1920-1930's, was the first model
to accurately predict the number and distribution of cases of an infectious disease as it is transmitted through a population over time. This theory led to the development of the
SIR models and their relatives that
are the mainstay of epidemiologists for predicting the behaviour of epidemics over time. The output of a typical SIR model looks like this:
The red curve corresponds to how many people are infected but have not recovered or died over time, the blue curve corresponds to how many people have not caught the virus yet over time, and the green curve corresponds to how many caught the virus and recovered, so are now immune.
The COVID-19 daily cases to date for Germany looks very similar to this SIR model prediction:
Howwver, the red curve in the SIR model is not describing quite the same thing as the red curve for the data from Germany: The data point in the data for Germany corresponds to the daily change in the sum of the red and green curves in the SIR model.
The connection between the SIR model and the data from Germany can be seen a bit better by looking at the daily cumulative data for Germany:
The red data in this chart the total number of cases reported over time. This corresponds to the sum of the red, green and purple curves in the SIR model:
Red = number of cases that have neither recovered or died yet
Green = number of cases that have recovered
Purple = number of cases that have died
or
Red + Green + Purple = number of cases that are either active, have recovered, or have died = number of reported cases
The sum of the red, green and purple curves of the SIR model looks remarkably like the actual number of cases reported for Germany over time, illustrating how well the
SIR model works.
There are several different SIR models that are based on different assumptions. Each of these models has a number of parameters that can be varied to change when the red curve peaks and how slowly the curve decays after that point. In order to fit a model to actual data the model's parameters need to be searched for the values that fit the actual data most accurately. Unfortuantely computing the SIR model output for a particular set of parameters is fairly complicated since these models are based on non-linear differential equations. Performing a search for the optimum parameters requires computing the model output many times, which can be quite time-consuming if you want to do that for all 210+ countries that are reporting data. Furthermore, the parameter values do not closely relate to the interesting features of the curves, such as when does the maximum in the number of cases occur and how many cases are there at that time.
Rather than trying to use a SIR model directly I elected to look for a simple mathematical function that would produce the same sort of pattern as a SIR model: an initial rapid exponential growth in the number of infected people, followed by a slowing in the growth rate until a maximum is reached, and then, at a slower rate, a decline in the number of new infected people.
The theory of SIR models has been developed over many years by epidemiologists in order to gain an understanding of how viruses spread. So you might think it is not right to look for some arbitrary function that produces similar looking results. But keep in mind that the goal here is not to understand how well a model based on some particular assumptions fits real data, but to see what the data is actually telling us. The issue here is that the assumptions of a SIR model may not be completely valid, so the predictions of that model may be off a bit, whereas an appropriate mathematical function unrelated to the SIR models might do a better job of actually fitting the real data in order to predict where the number of cases and deaths is headed in the immediate future.
The only standard function I found that seems to produce results similar to the SIR red curve above is the
Chi-Square Distribution. Unfortunately, this function is also complex to compute and understand. But, it is possible to devise a simple function that DOES reproduce the correct behavior. Consider one of the most popular distributions we all know about: the gaussian distribution, sometimes called the "bell curve", which looks like this:
The formula for a Gaussian Distribution is
For the chart above A = 1000, B = 50, and C = 10. The parameters are easy to interpret:
A = the value at the maximum of the peak
B = the location of the maximum
C = the half-width of the curve at approximately 33% of the maximum height
The problem with the Gaussian distribution is that it is symetrical about its maximum. So the rate at which it grows on the left side matches the
rate of decay on the right side. (Actually there are a few countries whose data actually looks very much like a Gaussian Distribution, probably because the
country was able to quickly completely contain the virus and take action to stop its growth.
What we are looking for is a similar formula that is asymetrical with a slower rate of decay than the rate of growth. A simple modification of the
Gaussian distribution produces the desired result:
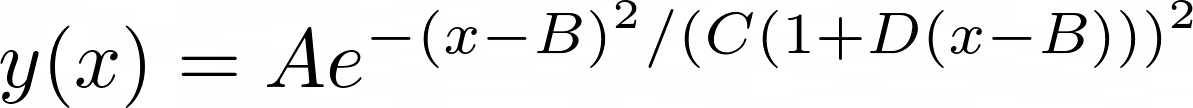
<--------(This is the model used on this website)
where D = 0 when x < B, so the function reduces to a the Gaussian distribution for x < B. Note that the
half-width of this new function to the left of the peak will be the same as the Half-width of the Gaussian Distribution with the same value of C, and the half-width to the right of the peak will be greater than the width of the Gaussian
Distribution. The new function looks like this for
D = 0.02 (Blue), D = 0.04 (Green) and D = 0.06 (Red):
These curves look like what we are after for modeling the number of daily new cases in data like shown above for Germany. The new parameter D, which we will call SKEW, determines how much slower the curve drops after the peak than it rises before the peak. But does actually realistically fit the data? Here is how it fits the data for Germany:
The model appears to fit the data extremely well. There is a lot of
scatter in the data because that is the nature of daily reporting, but the blue curve appears to pass through the middle of the data points. In this case the fit parameters are A = 5568
(height of the peak), B = 61.41 (between 4/2 and 4/3), C= 12.98 (the half width of the distribution if D were 0, and D = 0.1752, indicating the amount of skew.
Since we now have an equation that smoothly fits the reported daily cases from Germany, that equation can be used to project where the curve is headed with some certainty.
The number of cumulative cases is just the running sum of the daily cases, so it is easy to generate a chart of the cumulative cases for Germany:
Here again we see that the model fits the data extremely well.
SIR models also predict the number of deaths over time. The model presented here does the same. However, SIR models use the same parameters for predicting deaths that they use for predictng
cases, so they are limited in their flexibility to fit the progression of both cases and deaths at the same time. In looking at the real data for many different countries I noticed that the date of onset and
shape of the curve for daily deaths was typically a bit different than for cases, and there was no consistent pattern for these differences from one country to another. For that reason it seems best to
fit the data for deaths independently from the data for cases, resulting in a separate set of model parameters.The data and fit by the model for deaths in Germany looks like this:

The model fits the death data well too but with slightly different parameters: A = 231, B = 75.93, C = 16.38, and D = 0.1476. So, the peak occurs about 14.5 days later, grows a little slower than the number of cases, and decays a little faster. Although the
curves for cases and deaths looks fairly similar for Germany, that is not the case for some other countries, where the shape of the curves can be quite different.
The model makes no assumptions about WHY the particular shape of the curves for a country are the way they are - it just tells us WHAT they are. By comparing the curves for different countries the questions that epidemiologiests need to address become apparent: Why does the virus continue to spread rapidly in some countries while it seems to be significantly stopped in other countries? Why is the difference between the start of the exponential growth
for cases and deaths vary from one country to another? Why are the rates of decay in the number of cases and deaths different? Why are the number of cases per capita different for one country from another? Etc.
There are six regions of the world that WHO defines. For these regions and for the entire world the number of cases and deaths for the individual countries can be added to get regional or world numbers. However, the model cannot be applied to this regional and world data because the position of the peaks in the cases and deaths can occur at significantly different times so the summed data can have more than one peak. Because of that problem, the model cannot be fit directly to the regional or world data. Instead the individual fits for each country are added togeather, which provides a good fit to these more complex data.
A problem I ran into with the raw data was that they containe some discrepencies in the numbers that created some problem fitting the data with the model:
1) An obviously incorrect value can occur that is a typo because the daily amount on that day and the corresponding cumulative value do not agree. In this case the erroneous value was replaced by the correct value.
2) Reported data for a country may not be available for a particular day, in which case the data for the next day will represent two days of information. For the first day the values will be zero and for the second day the data will spike to approximately twice the normal height. In this case the data was spread evenly over the two days.
3) Occasionally a country will make a one-day correction to their cumulative numbers, resulting in a very large spike on that day that can be either positive or negative. In this situation the correction applies to the entire previous data, so it isn't clear how much of the correction applies to each of the previous days. In this case the correction amount was spread over all previous days and weighted by the original values on each of those days, so that days with higher initial values received larger corrections.
Although my model worked initially worked well fitting the country and state data with a single peak, it became apparent with time as regions started to relax their restrictions that a second peak emerged. I found that this problem could be overcome by fitting separate instances of the model to different time periods of the data, and once again I found that this allowed the multi-peak fits to accurately describe the data. One of the most outstanding examples of a double peak occurs for the number of daily cases in Iran, which you may want to take a look at. For a few countries and states I found that I needed to use three peaks to fit the data accurately. I expect that in the future I may need to use additional peaks, especially since a resurgence of COVID-19 is likely to occur in the winter.